遷移金属錯体の磁化率測定 ～磁化率，測定方法，遷移金属錯体～

 

こんにちは、trans(トランス)です。

今回は、遷移金属錯体の磁化率を測定し、特性を確認する実験について解説いたします。

 

まず、磁化率の章では、反磁性や常磁性などについて解説をいたします。

次に、測定方法の章では、磁化率の測定方法や磁化率の算出方法について解説いたします。

最後に、遷移金属錯体の章では、3d電子配置などについて解説いたします。

 

実験の予習をやらなければいけないけど時間が無いという学生に向けて、予習の手間が省けるように、この記事を書いています。スマホを見ながら電車で予習することもできます。実験項目は某大学の実験テキストを参考にしています。

レベル的には、大学の学部生レベルを想定していますが、高校生も化学の発展的なことに興味があれば、読んでみてください。

 

それでは行きましょう！

 

 

1、磁化率

 

磁場中に物質を置くと、その物質は磁気モーメントを持ちます。その単位当たりの磁気モーメントを磁化といいます。

また、磁化率χは、磁化Ｍと外部磁場Ｈの比例関係から以下の式で定義されます。

 

Ｍ＝χＨ…①

 

このときの磁化率はcgs電磁系において、無次元の物質量として扱われます。

 

1‐1、反磁性について

反磁性とは、外部磁場を弱める方向に磁化する性質のことです。このときはχ＜0であります。

ここで注意すべき点は、反磁性は、外部磁場への電子雲の応答であるから、全ての物質に存在するということです。

また、反磁性磁化率について、以下のパスカルの加成則が成り立ちます。

 

χ＝Σn_iχ_i＋Σｍ_kλ_k…②

 

n_i：分子内のi番目の同種原子の個数

χ_i：構成原子に割り当てられた磁化率

ｍ_k：ｋ番目の同種結合の個数

λ_k：結合の性質に依存する補正項

 

ここで磁化率χを扱いやすくするために、モル磁化率χ_mol(磁化率にモル体積をかけたもの、単位：cm³／mol)、グラム磁化率χ_g(χを密度で割ったもの、または、すなわちχ_gにモル質量をかけたものがχ_mol、単位：cm³／g)を定義します。

 

以下に代表的な原子および原子団の磁化率を示します。

 

 

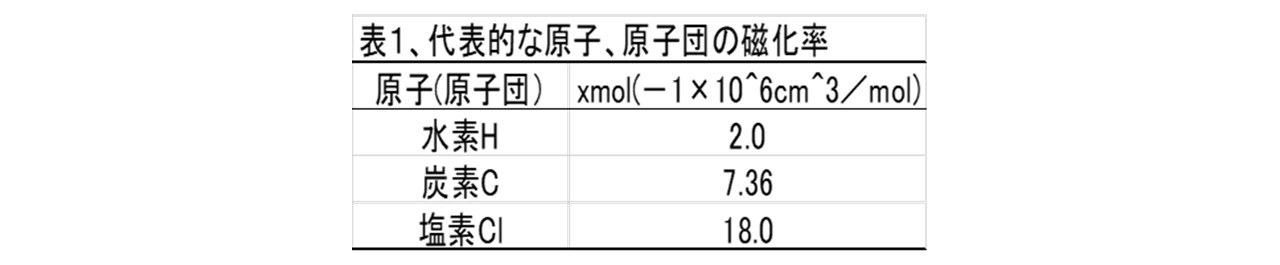
また、結合や原子団に対する補正項は以下の通りです。

 

 

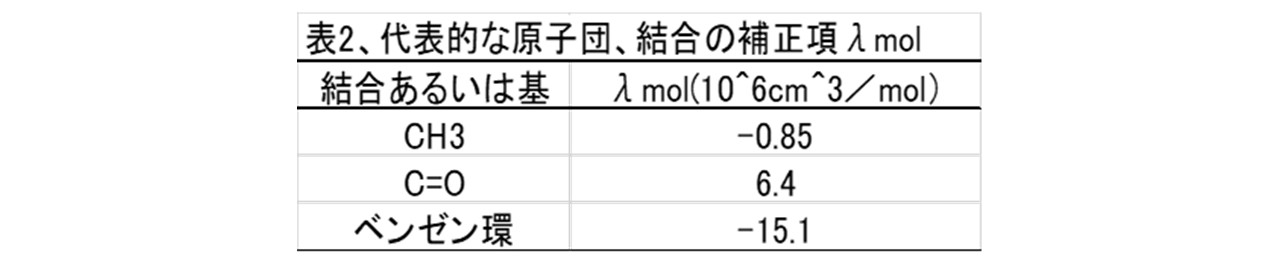
1‐2、常磁性

常磁性とは、磁場中で物質が外部磁場と同じ方向に磁化される性質のことです。このときは、x＞0であります。

常磁性は、外部磁場によって磁気モーメントの向きを変えることで生じます。これを永久磁気双極子モーメントといい、これは電子スピンと電子の軌道角運動量が原因で生じます。

このことから全角運動量Ｊｈ(－)は、電子スピンＳｈ(－)と軌道角運動量Ｌｈ(－)の和であるため、Ｊ＝Ｓ＋Ｌで示されます。

また、磁気モーメントと全角運動量の関係は以下のようになます。

 

μ＝ｇμ_ＢＪ…③

 

μ：磁気モーメント

ｇ：ランデのｇ因子

μ_Ｂ：ボーア磁子(＝ｅｈ(－)／2ｍ，ｍ：電子の質量)

Ｊ：全角運動量

 

式③から磁場Ｈ中の磁気モーメントのポテンシャルエネルギーは以下のようになります。

 

－μ・Ｈ＝－ｇμ_ＢＪ・Ｈ＝－ｇμ_Ｂｍ_JＨ…④

 

ｍ_J：Jの磁場方向成分

 

量子力学を用いると、ｍ_Jは、2J+1通りの値をとります。すなわち、ｍ_J＝±Ｊ，±(Ｊ－1)，．．．．，0となります。

熱力学観点から、熱平衡状態にある磁化Ｍの熱統計平均は、ボルツマン分布を用いると以下のようになります。

 

Ｍ＝Ｎｇμ_ＢΣ^J_mj＝－J(ｍ_Ｊｅｘｐ(ｇμ_Ｂｍ_ＪＨ／ｋＴ)／Σ^J_mj＝－J(ｅｘｐ(ｇμ_Ｂｍ_ＪＨ／ｋＴ)…⑤

 

Ｎ：単位面積あたりの個数

Ｔ：絶対温度

 

また、高温状態のときは、ｇμ_Ｂｍ_ＪＨ≪ｋＴと仮定でき、以下の式が得られます。

Ｍ＝Ｎｇ²μ_Ｂ²ＨＪ(Ｊ＋1)／3ｋＴ…⑥

 

式⑥を式①に代入すると以下のようになります。

χ＝Ｍ／Ｈ＝Ｎｇ²μ_Ｂ²Ｊ(Ｊ＋1)／3ＲＴ…⑦

 

式⑦をモル磁化率に換算すると以下のようになります。

χ_mol＝Ｎ_L²g²μ_Ｂ²Ｊ(Ｊ＋1)／3ＲＴ…⑧

 

Ｎ_L：ロシュミット数(アボカドロ数と同値)

 

有効磁気モーメントμ_eff、有効ボーア磁子数n_effを以下のように定義します。

 

μ_eff＝g(J(J+1))^1／2μ_Ｂ＝n_effμ_Ｂ…⑨

n_eff＝g(J(J+1))^1／2…⑩

 

式⑨を式⑧に代入すると以下のようになります。

χ_mol＝Ｎ_L²μ_eff²／3ＲＴ＝Ｎ_L²μ_Ｂ² n_eff²／3ＲＴ…⑪

 

式⑪から算出した実験的なボーア磁子数n_expは以下の通りです。

n_exp＝（3ＲＴｘ_mol／Ｎ_L²μ_Ｂ²）^1／2…⑫

 

磁気モーメントが、電子スピンＳｈ(－)で決まる場合、スピン・オンリーの式が成立するので、Ｌ＝０すなわち、Ｊ＝Ｓと置き換えることができます。また、Ｌ＝0のときのランデのｇ因子は2であり、これらのことから、Ｊ＝Ｓ、ｇ＝2を式⑩に代入すると以下のようになります。

n_eff＝2(Ｓ(Ｓ+1))^1／2…⑬

 

さらに、常磁性イオンの不対電子の数をnとすると、S＝(1／2)ｎとなり、この値を式⑬に代入すると以下のようになります。

n_eff＝2(1／2ｎ(1／2n+1))^1／2＝(ｎ(ｎ+２))^1／2…⑭

 

式⑫と式⑭を比較して、不対電子の数を推測することができます。

 

1‐3、強磁性と反強磁性

常磁性状態では、各磁気モーメントが孤立しているため、これらの間で相互作用が起きません。

このとき、以下のキュリーの法則が成り立ちます。

 

χ＝Ｃ／Ｔ…⑮

Ｃ＝Ｎg2μＢ2Ｊ(Ｊ＋1)／3ｋ(キュリー定数)…⑯

 

一方、磁気モーメント間の相互作用が無視できなくなると、キュリー・ワイスの法則で式⑮が以下のように示されます。

χ＝Ｃ／(Ｔ－θ)…⑰

 

このθはワイス定数(常磁性キュリー温度)といい、θ＞0のときに磁気モーメント間の相互作用が強磁性で、θ＜0のときに磁気モーメント間の相互作用が反強磁性です。

強磁性とは、隣り合う磁気モーメントが同方向に並んだ方がエネルギー的に有利であるということで、反強磁性は逆の方向に並んだ方がエネルギー的に有利であることです。

磁気モーメント間の相互作用は、基本無視できますが、温度が十分に低く、磁気相転移温度以下になったときには注意する必要があります。

 

 

2、測定方法

 

ここからは、磁化率の測定方法について解説していきます。

 

2－1、電子天秤について

本実験では、エバンス法を用いていますが、基本的にはグーイ法に基づいているため、まずグーイ法について説明します。

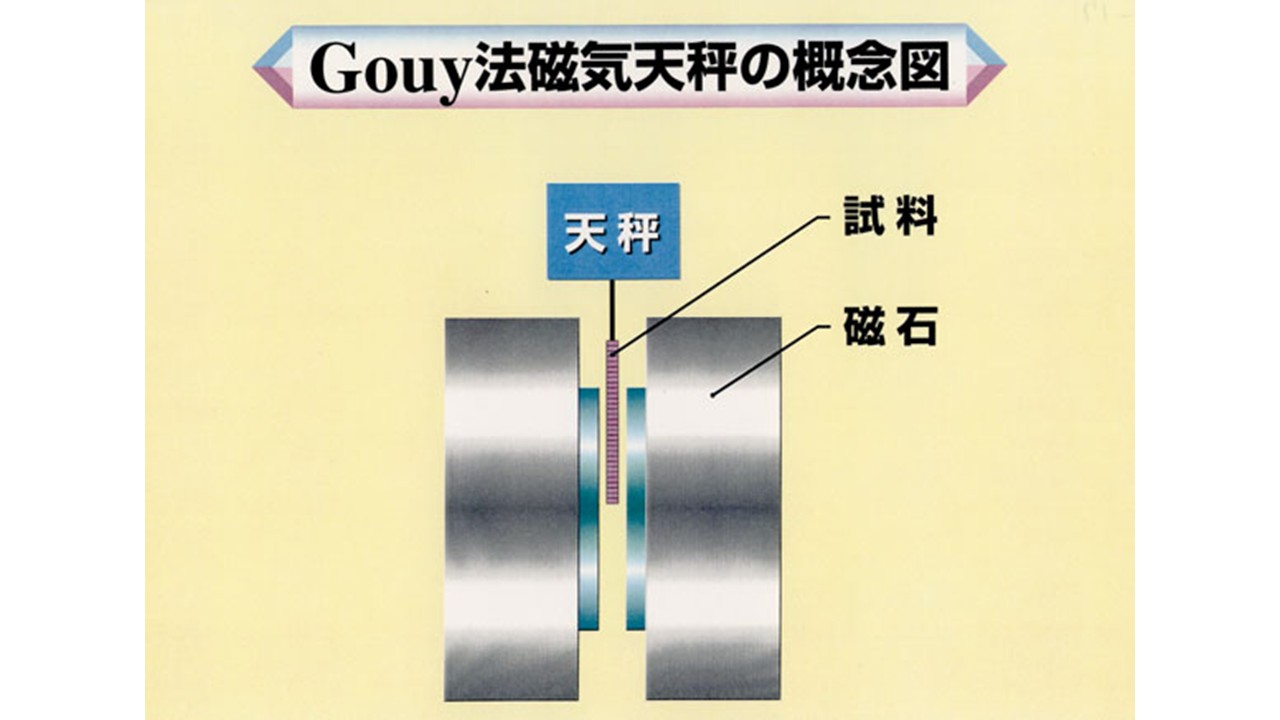
グーイ法による磁化率測定装置は以下のようになっています。

 

引用：パターン9-17、Ｇｏｕｙ法磁気天秤の概念図

 

上に示したように、試料管中の試料は下方が均一な強い磁場H0がかかっている領域にあり、上方が強い磁場を受けない領域にあるように天秤につるされています。試料と磁場の相互作用で、縦方向（z軸方向）に試料が力を受けます。

この力は、磁場によって試料の体積Δvで生じた磁気モーメントＭ(ｚ)Δｖが不均一磁場Ｈ(ｚ)の中で、磁場勾配によって受ける力Ｍ(ｚ)Δｖ(ｄＨ／ｄｚ)によるものであります。ここでＭ(ｚ)は、磁化であるので式①を用いると以下のようになります。

 

χ＝Ｍ(ｚ)／Ｈ(ｚ)…⑱

 

ここでｚ軸上にあり、体積Δｖの試料のポテンシャルエネルギーΔＡ(ｚ)は、Δｖをｚ軸方向に、磁場がないところまで移動するのに必要な仕事の符号を入れ替えたものであるので、以下のように示されます。

 

 

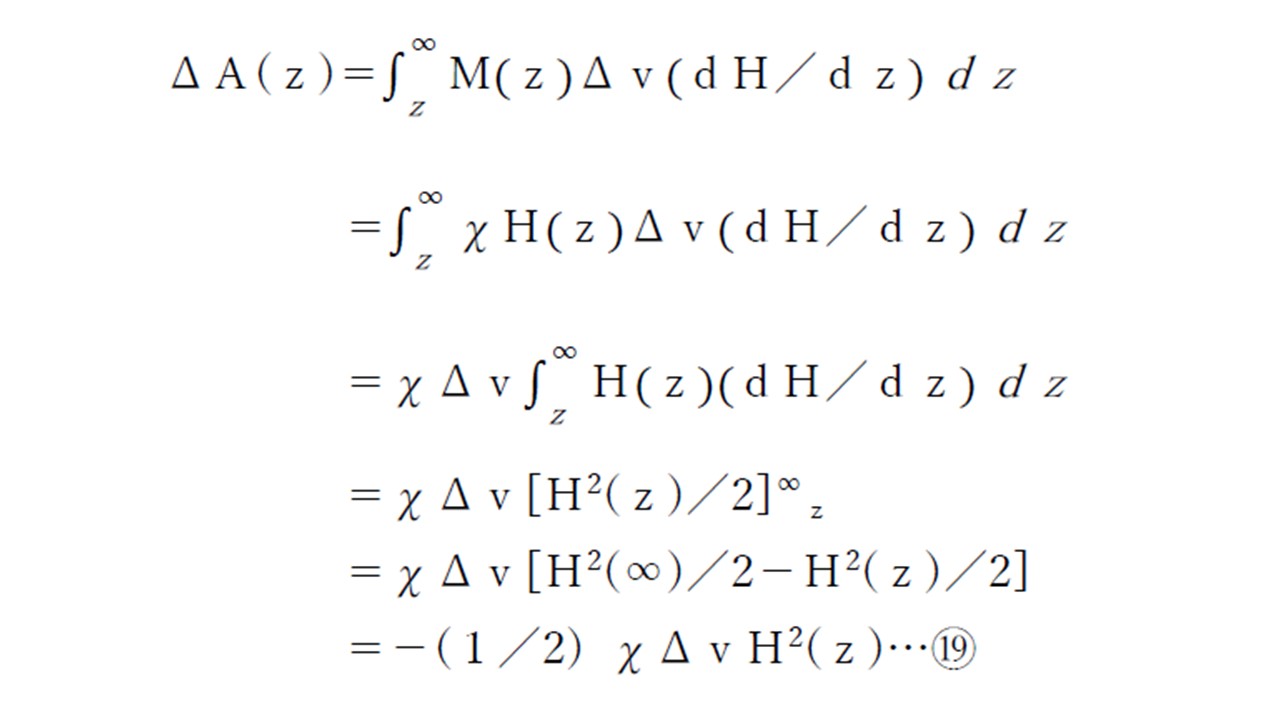
Δｖに働く力ΔＫは、ポテンシャルエネルギーの勾配の符号を変えたものであるので以下のようになります。

ΔＫ＝－(ｄΔＡ(ｚ)／ｄｚ)＝(１／2)χΔｖ(ｄＨ2(ｚ)／ｄｚ)…⑳

 

また、試料全体に働く力Ｋは、式⑳を積分すればよいので以下のようになります。

㉒式から分かるように磁場と試料の相互作用による力は、磁化率に比例します。

すなわち、この比例定数－(１／2) aＨ²₀を求めれば、未知試料の磁化率を求めることができます。

 

 

ここからは、エバンス法について説明いたします。

先ほど述べたグーイ法と基本的に変わりませんが、グーイ法では磁石を固定していたのに対し、エバンス法では試料を固定し、ワイヤーで橋渡しされた2個の磁石の一方により引かれる力を測定します。

ここで得られる力も原理的には、グーイ法と同じであるので、こちらも式㉒の比例定数を求めればよいことが分かります。

 

2－2、磁化率の算出法

先ほど記したように、式㉒の比例定数－(１／2) aＨ²₀を求めれば、未知試料の磁化率を求めることができます。

質量ｍの試料を入れた試料管を磁気天秤へ挿入して得られた表示値をＲ、空の試料管を磁気天秤へ挿入して得られた表示値をＲ₀として、比例定数ｋとすると以下のように示すことができます。

ｋ(Ｒ－Ｒ₀)＝－(１／2) χaＨ²₀…㉓

 

試料の密度をｄ、試料の断面積をa、試料の長さをlとするとｄ＝ｍ／alとなります。また、χ_ｇ＝χ／ｄであるので、式㉓の右辺は以下のように変形できます。

ｋ(Ｒ－Ｒ₀)＝－(１／2) χ_g(ｍ／al)aＨ²₀

＝－(１／2) χ_g(ｍ／l)Ｈ²₀…㉔

 

式㉔をχ_gの形にすると以下のようになります。

χ_g＝(l／m)(－2k／Ｈ²₀)(Ｒ－Ｒ₀)…㉕

 

この－2k／Ｈ²₀を天秤定数Ｃと置けば以下のようになります。

χ_g＝(l／m)Ｃ(Ｒ－Ｒ₀)…㉖

 

また、ここまでの解説では試料と空気の置き換わりの補正、すなわち、空気の補正について述べていなかったので、それについても説明いたします。

空気の磁化率をχ_airとして式㉓に対応させると以下のようになります。

ｋ(Ｒ－Ｒ₀)＝－(１／2)(χ－χ_air)aＨ²₀…㉗

 

これを、χ＝の形に変形すると以下のようになります。

χ－χ_air＝(－2k／aＨ²₀)(Ｒ－Ｒ₀)＝(Ｃ／ａ)(Ｒ－Ｒ₀)

　　　χ＝(Ｃ／ａ)(Ｒ－Ｒ₀)＋χ_air…㉘

 

式㉘をχ_ｇに変形すると以下のようになります。

χ_ｇ＝χ／(ｍ／ａｌ)＝(ｌ／ｍ){Ｃ(Ｒ－Ｒ₀)＋aχ_air}…㉙

 

また、空気の磁化率は、ｘ_air＝0.029×10^－6(20℃、700mmgＨｇ)としました。

本実験の計算において、式⑫を用いますが、計算を楽にするために、以下のように近似します。

n_exp²＝（3ＲＴ／Ｎ_L²μ_Ｂ²）ｘ_mol≒8Ｔχ_mol…㉚

 

また、式⑭のn=の変形においては以下のようにしました。

n_eff²＝ｎ(ｎ+２)

n_eff²＋１＝ｎ^２＋２ｎ＋１

n_eff²＋１＝(ｎ＋１)^２

√n_eff²＋１＝ｎ＋１

　　　ｎ＝－１＋√(n_eff²＋１)…㉛

 

 

3、遷移金属錯体

 

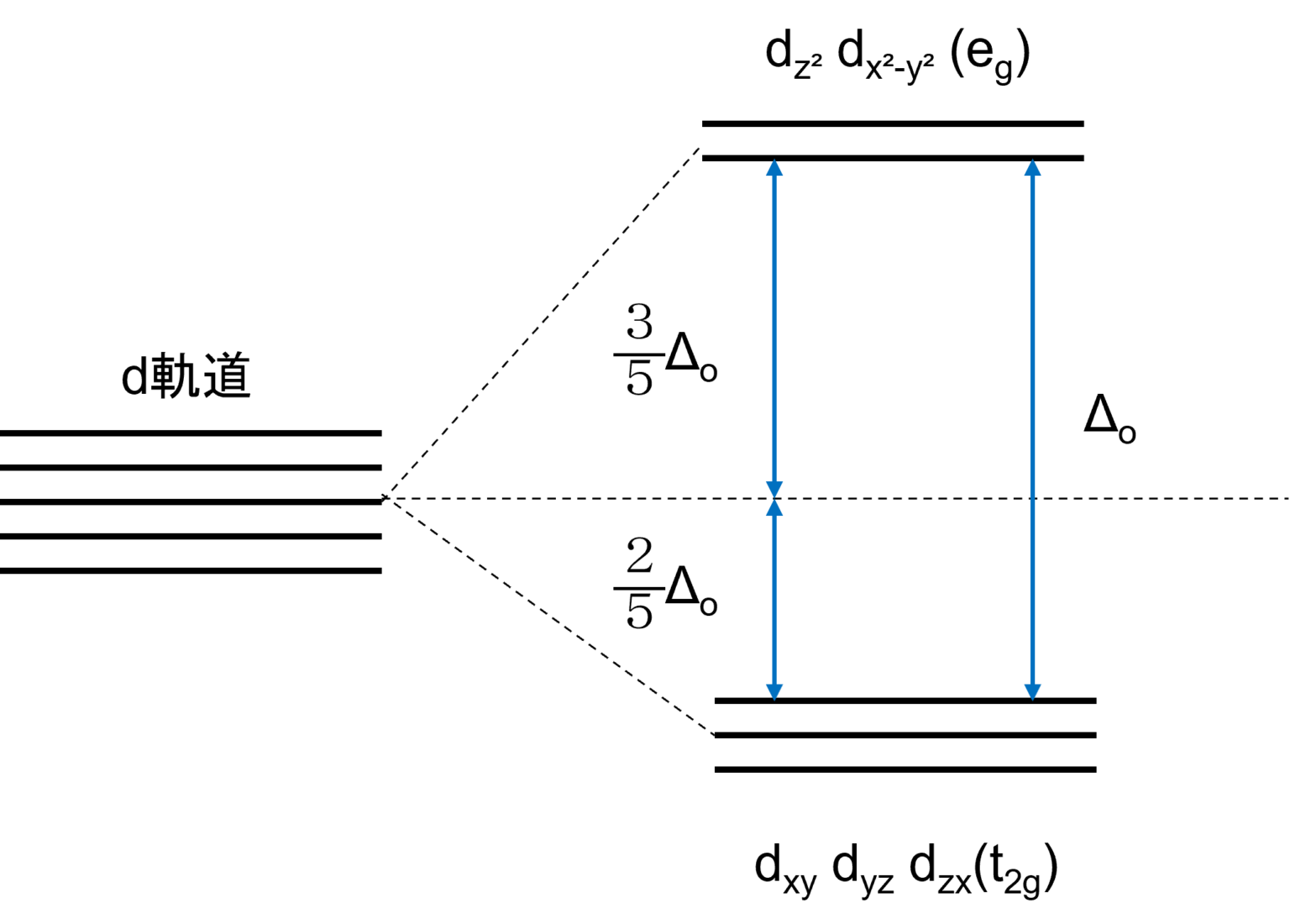
正八面体結晶場中の遷移金属イオンのｄ電子配置と結晶場の強さとの関係は結晶場理論を用いて説明することができます。

通常d軌道の５つは等しいエネルギーで5重に縮退しています。しかし、結晶場理論において、x軸、y軸、ｚ軸の両端方向から6個の配位子が負の点電荷として存在し、近づいてくると考えます。

このような事を考えると軌道の形によって安定性が変わります。

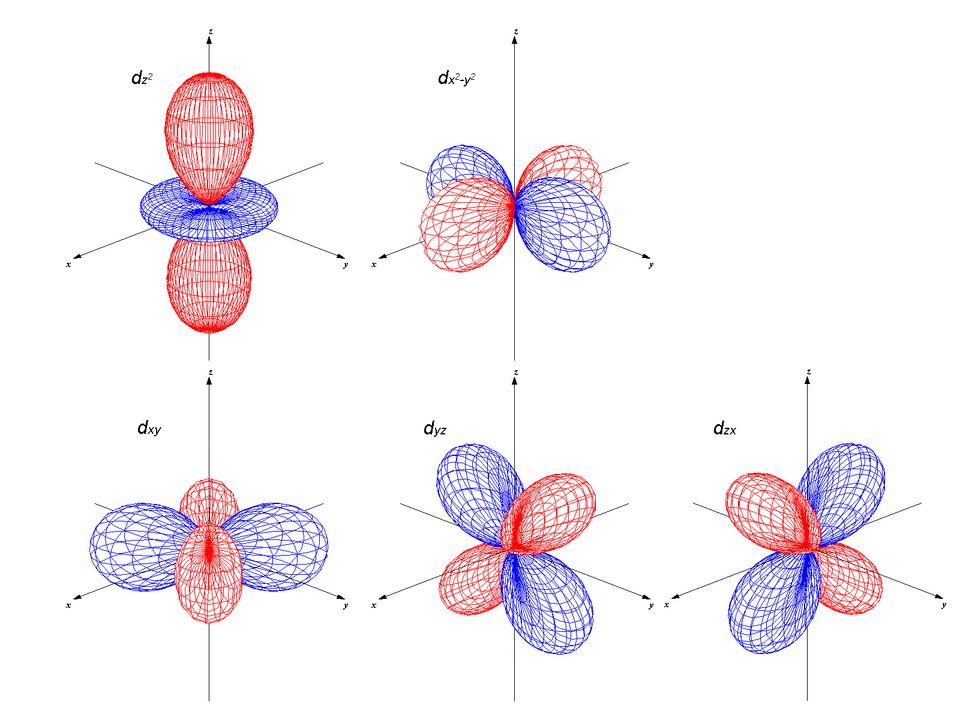
以下に、d軌道5つを示します。

 

引用：d軌道 ー Wikipedia

 

ここでｄz2、ｄx2－y2を考えると直交軸に対する配位子の方向に、電子密度が高く、電子同士が反発します。

このため、この2つの軌道はエネルギー的に不安定であることが分かります。このような2つの軌道をeg縮退軌道といいます。

 

一方、ｄzx、ｄyz、ｄxyを考えると直交軸に対する配位子の方向に、電子密度が低く、電子同士が反発しづらいです。このため、この3つの軌道はエネルギー的に安定であるといえます。このような3つの軌道をｔ2g縮退軌道といいます。

 

このような事から、正八面体結晶場中のd軌道のエネルギーは以下のように示すことができます。

 

引用：[院試頻出]結晶場理論におけるd軌道分裂の考え方

 

このeg縮退軌道とｔ2g縮退軌道のエネルギーの差のことを、配位子場分裂パラメーターといいます。

また、電子の入り方としては、フント則に従い、3つまではｔ2g縮退軌道に入ります。問題は、4つ目以降の電子であって、これは配位子の分光化学系列によって決められます。

分光化学系列が大きいと配位子場分裂パラメーターが大きくなり、そのためｔ2g縮退軌道に入って低スピン錯体になります。一方、分光化学系列が小さいと配位子場分裂パラメーターが小さくなり、そのためeg縮退軌道に入った方が電子同士のスピン生成エネルギーよりも安定であるため、高スピン錯体になります。

 

 

4、～まとめ～

いかがでしたか？

今回は、遷移金属錯体の磁化率を測定し、特性を確認する実験について、磁化率，測定方法，遷移金属錯体という3つのキーワードから説明しました。どの章も重要なのでしっかりと抑えておきましょう。

 

また、参考文献は以下の通りになります。

１、日本化学会編，新実験化学講座３基礎技術２，丸善（1976），p.43～76

 

最後になりますが、参考文献以外はコピペ厳禁です。バレます。気を付けてください。自分で理解してまとめてください。

 

また、完全に情報を網羅しきれていないと思いますので、質問等ありましたら、下のコメント欄にコメントお願いします。

今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。