こんにちは、trans(トランス)です。
今回は、二酸化炭素の気圧を変えた時の状態変化の実験と気体の状態方程式を用いた二酸化炭素の分子量測定の実験について紹介します。
まず、二酸化炭素の章では、今回の状態変化や分子量測定の実験で、なぜ二酸化炭素が用いられるかの理由や二酸化炭素の物理定数などの基本情報を説明します。
次に、相図の章では、相図とは何かという基本的なことを、物質の三態や相転移といったことと関連させながら説明していきます。
さらに、理想気体の状態方程式の章では、今回の実験で得られたデータから分子量を測定する方法や、理想気体と実在気体の違いから今回の実験で生じた誤差について考察をしていこうと思います。
実験の予習をやらなければいけないけど時間が無いという学生に向けて予習の手間が省けるように、この記事を書いています。スマホを見ながら電車で予習することもできます。実験項目は某大学の実験テキストを参考にしています。
レベル的には、大学の学部生レベルを想定していますが、高校生も化学の発展的なことが知りたければ読んでいただいて構いません。
それでは行きましょう!
1、二酸化炭素

二酸化炭素とは、炭素Cと酸素Oの化合物のことで、空気中に0.04 %ほど含まれる気体のことです。
今回の実験において二酸化炭素が重要である点は、昇華性にあります。昇華とは、物質の状態変化のひとつで固体から気体、または気体から固体になるときの状態変化のことをいいます。また、固体の二酸化炭素をドライアイスといい、保冷剤として利用されます。
つまり、ドライアイスをフラスコ内にいれて完全に昇華させ二酸化炭素にするとフラスコ内を空気から二酸化炭素に置換することができます。これと理想気体の状態方程式を利用すると二酸化炭素の分子量を測定することができます。
また、気圧の条件を変えて二酸化炭素を観察すると気体と固体ではなく液体の二酸化炭素を確認することもできるので、この実験を基にして相図の知識を確認することができます。
この章の最後に二酸化炭素の物理定数をいくつか下に示します。
化学式:CO₂
モル質量:44.01 g/mol
外観の状態:無色の気体
融点:-56.6 ℃
沸点:-78.5 ℃
2、相図

相図(そうず)ということなので麻雀の索子(ソーズ)とかけてみました。分からない人はスルーで全然大丈夫です。
物質は固体、液体、気体と3つの状態変化を持ちます。これを物質の三態といいます。
また、純物質は、温度を上げていくと固体→液体→気体の順(昇華性のあるものは固体→気体)に変化していきます。このときに各状態変化の境目(融点,沸点)は決まっています。しかし、温度以外にも気圧(圧力)によっても状態変化が起こります。この温度と圧力の関係性とそのときの状態を図にしたものを相図といいます。例として、二酸化炭素相図を下に示します。
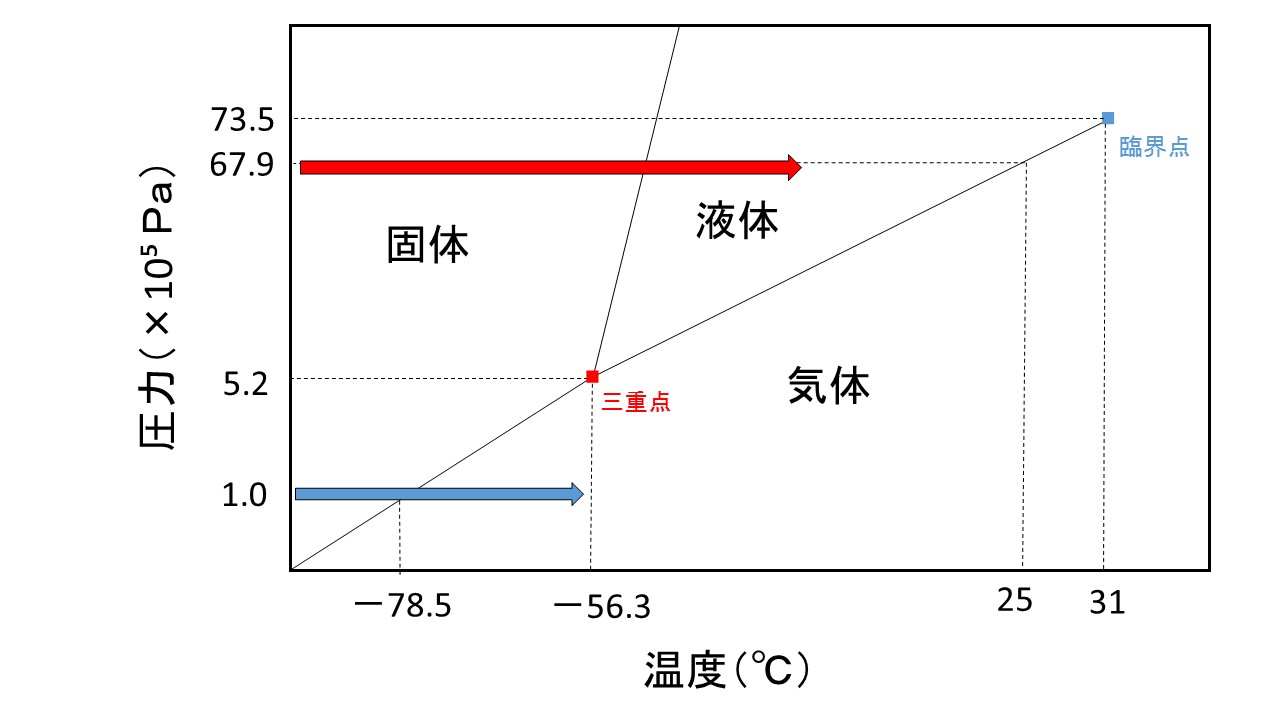
上記の相図に斜めの線が入っていることが分かると思います。この線によって固体,液体,気体の3つのブロックに分かれています。このような各ブロックを相と呼びます。つまり、この線は各状態の境界線にあります。この状態が変化するとき、すなわち境界線を越えて別の相に移動することを相転移といいます。
また、赤い点で示した3つの線が交わる点を三重点といいます。この三重点では3つの状態が混在しているため、3つの状態が共存しています。
さらに、青い点で示した線が途切れたところを臨界点といいます。この臨界点を越えた領域では、気体と液体の両方の性質を持つような超臨界流体という状態で存在します。
上記の相図から分かるように、通常の気圧(1.0×10⁵ Pa)のときは青矢印のような温度変化が起こるので、二酸化炭素は通常は固体と気体の状態でしか存在しません。しかし、圧力を67.9 ×10⁵ Paまで上げると赤矢印のような温度変化が起こります。すなわち常温(25 ℃)で気体と液体が混在した状態を観察することができます。
本実験では、このような原理によって圧力を上げることで通常では見ることのできない二酸化炭素の液体状態を見ることができます。
3、理想気体の状態方程式

気体ということで雲の画像を載せました。まあ、それだけです(笑)。
ボイル・シャルルの法則とは、一定量の体積(L)は圧力(Pa)に反比例し、絶対温度(K)に比例するという法則で、V:体積,p:圧力,T:温度とすると以下のような関係式が得られます。

ここからは、真ん中の p’V’/T’ を除いて話をしていきます。上記の関係式が成り立つとき、1モルあたりの体積をv(L/mol),定数をR(Pa・L/mol・K)として代入して、両辺にTをかけると以下の式を算出することができます。
pv = RT ・・・・・・①
化学基礎の復習になりますが、標準状態(T=273 K,p=1.0×10⁵ Pa)のときの1モルあたりの体積は、22.4 Lですね。つまり、これで①式のR以外の全ての文字が分かったので、Rの値を算出することができます。ちなみに、R=8.31×10³ (Pa・L/mol・K)です。
また、1モルあたりの体積v(L/mol)は、体積V(L)を物質量をn(mol)で割った値なので、v=V/n と表すこともできます。これを①式に代入し両辺にnをかけると、以下のような理想気体の状態方程式を算出することができます。
pV = nRT ・・・・・・②
また、物質量n(mol)はモル質量(g/mol)で質量(g)を割って算出することができるので、モル質量をM,質量をmとすると、n=m/M と表すことができます。②式に代入すると以下のようになります。

この両辺にMをかけると以下のようになる。

さらにM=の形にするために両辺をpvで割ると、以下のような分子量を算出する式を得ることができます。Mはモル質量のことですが、分子量はモル質量の単位がないバージョンのことなので、このまま下の式を使うことができます。

分子量を実験から得た結果から算出すると多くの場合、44に近い値ではあるものの44にはならず、誤差が生じると思います。なので最後に、理想気体と実在気体の違いから今回の実験で生じた誤差について考察します。
理想気体とは、分子自体の体積がなく、分子間力が存在しないと仮定したときの気体のことです。気体がこのような理想気体であったときに、気体の状態方程式は成り立ちます。
しかし、当然のことですが、分子には体積があり、気体の分子間には分子間力が働きます。このような実際に存在する気体のことを実在気体といいます。つまり、実在気体の体積は観測される体積より分子自体の体積だけ小さくなります。また、圧力は分子が壁に衝突する回数によって決まるので、実際に観測される圧力は、実在気体の圧力よりも分子間力分減少します。
よって、実際に観測される体積 V は、実在気体の体積 V’ と分子自体の体積 V₀ の和になります。したがって、V=V’+V₀ という関係式が導かれます。実際に状態方程式で用いる体積は実在気体の体積であるので、V’=V-V₀ を用います。
また、実際に観測される圧力 p は、実在気体の圧力 p’ が分子間力により減少した圧力 p₀ だけ減少した値になります。したがって、p=p’-p₀ という関係式が導かれます。実際に状態方程式で用いる圧力は実在気体の圧力であるので、p’=p+p₀ を用います。
この2つのことを考慮すると以下のような実在気体の状態方程式を導くことができます。
(V-V₀)(p+p₀)=nRT
また、V₀とp₀ を、それぞれパラメーター(実用性がある換算係数をかけたもの,今回はこれ以上の説明を省略します)に変換すると以下のよう状態方程式を導くことができます。この式はファンデルワールスの状態方程式といいます。
(V-nb){p+(n/V)²・a}=nRT
このような実在気体と理想気体のずれによって誤差が生じたと考えられます。その他にも、実験操作による誤差も考えられますが、基本的には実在気体と理想気体のずれを考察のメインにすると良いと思います。
4、~まとめ~
いかがでしたか?
今回は、二酸化炭素の状態変化と分子量測定の実験について紹介しました。
特に、相図の関係性や理想気体の状態方程式,理想気体と実在気体の違いは、大切な項目なので予習をしっかりと行っておきましょう。
また、参考文献は以下の通りになります。
1、辰巳敬(他13名)「化学」数研出版、2012、p 35,45~49,54~55
2、戸嶋直樹,瀬川浩司「理解しやすい化学」文英堂、2012、p 192~193
最後になりますが、参考文献以外はコピペ厳禁です。バレます。気を付けてください。自分で理解してまとめてください。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。